Buckling resistance
The buckling resistance is given by the formula
![]()
Where is: | χ |
|
A |
| |
fy |
| |
γM1 |
|
The area of the effective cross-section is used for the class 4. The value of Aosl is used for perforated cross-sections. The buckling resistance is calculated for directions y and z or for the main axes directions η and ζ (L-cross-sections).
The values of slenderness λz and λy for buckling perpendicular to the axes z and y are given by expression
![]()
Where is: | Lcr,z, Lcr,y |
|
iz, iy |
|
The values of relative slenderness ![]() and
and ![]() are given by the expressions
are given by the expressions
![]()
Where is: | λz, λy |
|
λ1 |
| |
Aeff |
| |
A |
|
The slenderness value to determine the relative slenderness λ1 is given by the formula
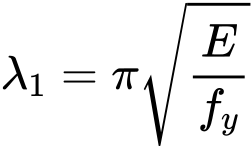
Where is: | E |
|
fy |
|
The value of imperfection factor α is selected according to the values ![]() and
and ![]() and shape of the cross-section. This factor represents one of the buckling curves a0, a, b, c, d. The buckling curve may be also selected by the user. The reduction factors for buckling χz and χy are calculated using expressions
and shape of the cross-section. This factor represents one of the buckling curves a0, a, b, c, d. The buckling curve may be also selected by the user. The reduction factors for buckling χz and χy are calculated using expressions
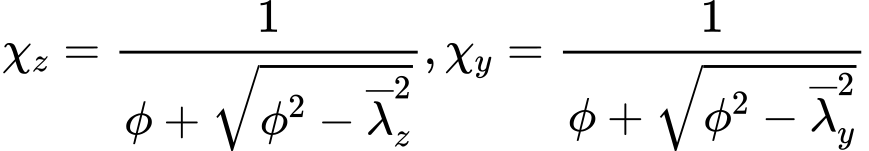
however, following expressions have to be fulfilled
![]()
where ϕ is calculated according to the follwoing expressions for directions z and y.
![]()
The buckling resistances Nb,Rd,z and Nb,Rd,y are calculated with the help of reduction factors χz and χy:
![]()
The design value of the buckling resistance is reduced for "High shear" (described in the chapter "Low and high shear"). The reduction factor is given by the expression
![]()
Where is: | ρz,ρy |
|
AV,z,AV,y |
| |
A |
|