Calculation of resistance
The resistance of structures in fire situations is affected by the reduction of strength and deformation properties caused by increased temperature. These changes are described by reduction factors ky,θ and kE,θ. ky,θ is the reduction factor for the yield strength and kE,θ is the reduction factor for the slope of the linear elastic range. Values are given in EN 1993-1-2, interval is between 1.0 for 20°C and 0.0 for 1200°C. Thus, the verification of steel elements is based on reduced values of yield strength and modulus of elasticity.
Calculation of shear resistance
The shear resistance for directions z and y is calculated using expressions
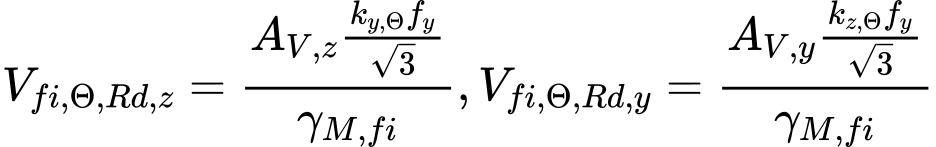
Where is: | AV,z, AV,y |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
If the corresponding plate of the cross-section are fixed on both ends in the perpendicular directions, the effect of local buckling is taken into consideration. The effect of the local buckling may be reduced with the help of web stiffeners. The simple post-critical method is used for the buckling of walls:
![]()
Where is: | d |
|
tw |
| |
τba |
| |
γM,fi |
|
The design shear resistance Vfi,θ,Rd,z is calculated as the minimum of Vfi,θ,Rd,z and Vfi,θ,ba,Rd,z, the design shear resistance Vfi,θ,Rd,y is calculated as the minimum of Vfi,θ,Rd,y and Vfi,θ,ba,Rd,y. The buckling caused by shear isn't considered for plates supported only on one end.
Shear due to torsion
The St. Venant and warping torsion is considered during the analysis. For St. Venant torsion, the shear stress τt is calculated for torsional moment Tt. Following expression is used for open cross-sections:
![]()
Where is: | Tt |
|
It |
| |
t |
|
The stress τt for closed cross-sections is given by the expression
![]()
Where is: | Tt |
|
Ωt |
| |
t |
|
For warping torsion, the shear stress τω is calculated for torsional moment Tω using following formula:
![]()
Where is: | Tω |
|
Sω |
| |
Iω |
| |
t |
|
The shear stress is verified according to the following expression:
![]()
Where is: | ky,θ |
|
fy |
| |
γM,fi |
|
The values of shear resistance VRd,y and VRd,z are reduced due to torsion for combination of shear forces and torsional moments. The reduction is based on following expression
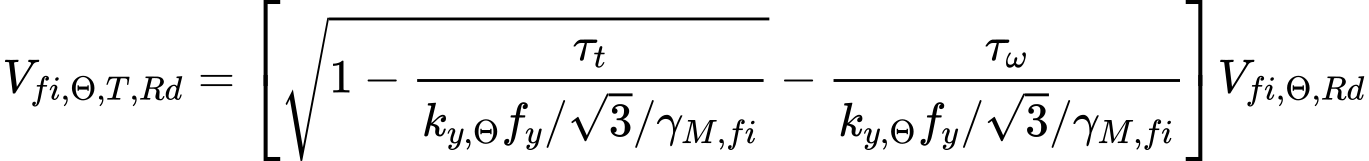
for I- and U-profiles and
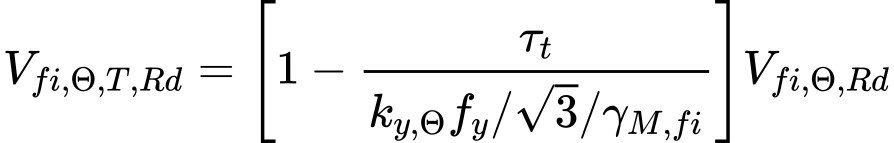
for other cross-sections.
Calculation of tensile resistance
The tensile resistance is calculated using the expression
![]()
Where is: | A |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Calculation of compressive resistance
The compressive resistance is calculated using the expression
![]()
Where is: | A |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Calculation of compressive resistance including buckling consideration
The compressive resistance is calculated using the expression
![]()
Where is: | χfi |
|
A |
| |
ky,θ |
| |
fy |
| |
γM,fi |
|
The resistance including buckling consideration is calculated in directions y and z or in directions of main axes η and ζ. The reduction factor for flexural buckling χfi corresponds to the relative slenderness ![]() and is given by the expression
and is given by the expression
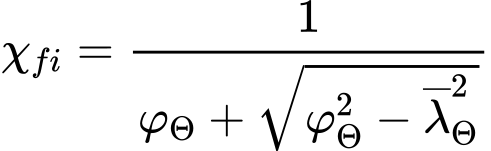
where
![]()
where
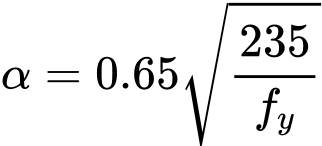
The relative slenderness ![]() for the temperature θ is given by the expression
for the temperature θ is given by the expression
![]()
Where is: |
|
|
ky,θ |
| |
kE,θ |
|
The minimum of values for both directions is considered as the compressive resistance Nb,fi,θ,Rd.
Calculation of bending resistance
The flexural resistance is calculated using the expression
![]()
Where is: | W |
|
ky,θ |
| |
fy |
| |
γM,fi |
| |
κ1 |
| |
κ2 |
|
The bending resistance is calculated in four points (corners of the cross-sections) for cross-sections in classes 3 and 4.
Effect of lateral-torsional buckling
The flexural resistance including an effect of lateral-torsional buckling is calculated using the expression
![]()
Where is: | χLT,fi |
|
Mc,fi,θ,Rd |
|
The reduction factor for lateral-torsional buckling χLT,fi corresponds to the relative slenderness ![]() and is given by the expression
and is given by the expression
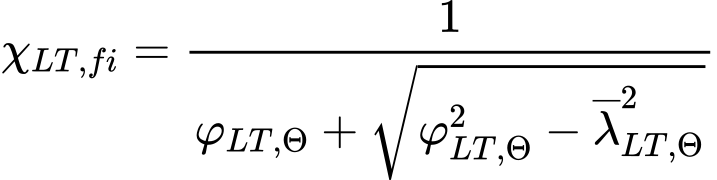
where
![]()
where
The relative slenderness ![]() for the temperature θ is given by the expression
for the temperature θ is given by the expression
![]()
Where is: |
|
|
ky,θ |
| |
kE,θ |
|
Calculation of resistance for bimoment
The stress caused by the bimoment is calculated with the help of elastic theory. Therefore, these cross-sections are automatically designed as classes 3 or 4. The resistance is calculated in four points (corners of the cross-sections), where are the worst results expected. The resistance is calculated using following expression:
![]()
Where is: | Iω |
|
ω |
| |
ky,θ |
| |
fy |
| |
γM,fi |
| |
κ1 |
| |
κ2 |
|