Influence of water
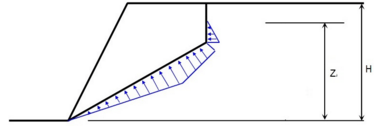
By default, the program performs the stability analysis of a rock wedge without considering groundwater. If interested in the influence of groundwater on a rock wedge it is necessary to introduce the height of GWT from the line of intersection of slip surfaces and rock face (the GWT takes an arbitrary position over the entire height of a rock wedge). The program assumes that water can flow freely discontinuities located below the GWT (no restrictions, e.g. due to ice blocks, are considered).
The water pressure acts in the direction normal to the slip surfaces against normal components of the passive forces. If the height yw above the point of maximal pressure Pmax is equal or larger than Z/2 and it is fully contained by the rock wedge, then its value is assumed to be equal to Z/2 (case A). If the height yw above the point of maximal pressure Pmax is less than Z/2 (case B), then its value reduced as:
![]()
where: | L* | - | length of the line intersection of slip surfaces A1, A2 |
α1 | - | gradient of rock face | |
δ | - | gradient intersection line of the slip surfaces |
The resulting water pressure on slip surfaces 1 and 2 is given by:
![]()
![]()
where: | Z | - | height of GWT above the line of intersection of slip surfaces and rock face |
Pmax | - | maximal water pressure on the line of intersection of slip surfaces | |
γw | - | unit weight of water (≈ 10 kN/m3) | |
A1w | - | are of the wetted part of the slip surface 1 | |
A2w | - | area of the wetted part of the slip surface 2 |
 Distribution of water pressure on the line of intersection of slip surfaces
Distribution of water pressure on the line of intersection of slip surfaces
If a tension crack is found either entirely or partially below the GWT, then the influence of water pressure is reflected both on slip surfaces 1 and 2 through forces P1and P2acting on the intersection of these surfaces and on tension crack through force P3 acting in the direction normal to the tension crack.
 Distribution of water pressure when considering GWT in tension crack
Distribution of water pressure when considering GWT in tension crack