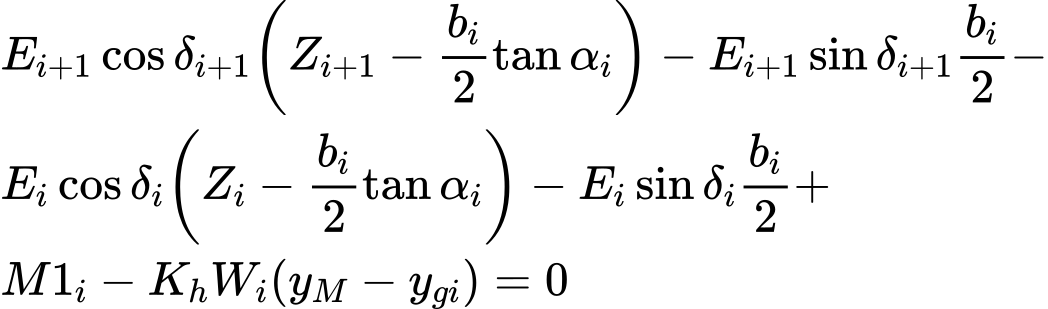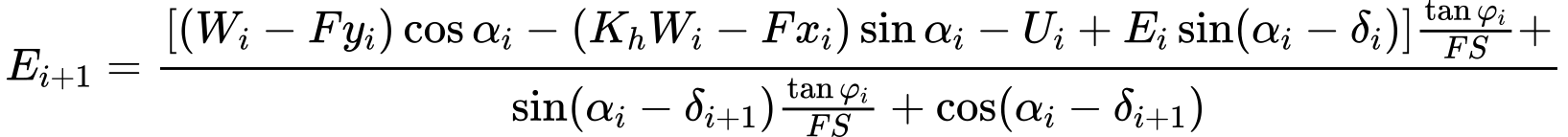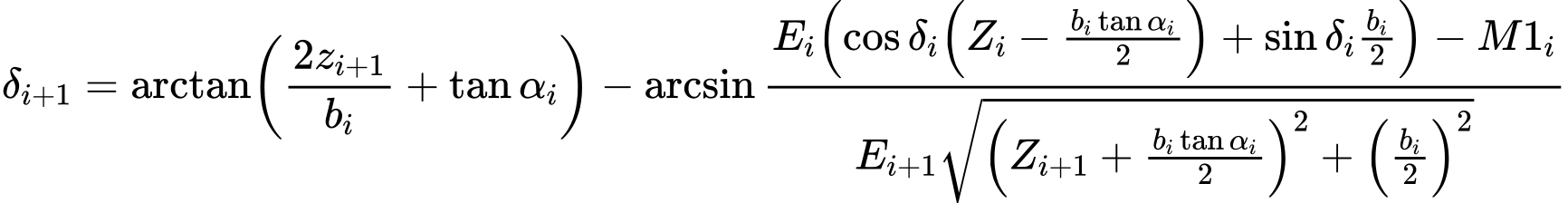Janbu
Janbu is a general method of slices developed on the basis of limit equilibrium. It requires satisfying equilibrium of forces and moments acting on individual blocks (only moment equilibrium at last uppermost block is not satisfied). The blocks are created by dividing the soil above the slip surface by dividing planes. Forces acting on individual blocks are displayed in the following figure:
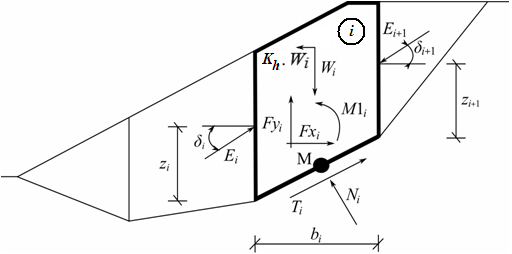 Static scheme - Janbu method
Static scheme - Janbu method
Each block is assumed to contribute due to the following forces:
Wi | - | block weight, including material surcharge having the character of weight including the influence of the coefficient of vertical earthquake Kv |
Kh*Wi | - | horizontal inertia force representing the effect of the earthquake, Kh is the factor of horizontal acceleration during earthquake |
Ni | - | normal force on the slip surface |
Ti | - | shear force on the slip surface |
Ei ,Ei+1 | - | forces exerted by neighboring blocks, they are inclined from the horizontal plane by an angle δi resp. δi+1 and lie at the height zi resp. zi+1 above slip surface |
Fxi,Fyi | - | other horizontal and vertical forces acting on the block |
M1i | - | moment from forces Fxi, Fyi rotating about point M, which is the center of the ith segment of the slip surface |
Ui | - | pore pressure resultant on the ith segment of the slip surface |
The following assumptions are introduced in the Janbu method to calculate the limit equilibrium of forces and moment on individual blocks:
- dividing planes between blocks are always vertical
- the line of action of the weight of block Wi passes through the center of the ith segment of slip surface represented by point M
- the normal force Ni is acting in the center of the ith segment of slip surface, at point M
- position zi of forces Ei acting between blocks is assumed, at slip surface endpoints is z = 0
The choice of position zi can have significant influence on the convergency of the method. If we make a bad assumption of position zi for a given slope, it can become impossible to satisfy the equilibrium conditions (algorithm does not converge). Heights zi above the slip surface are set approximately to one third of the height of interface between the blocks. In case of unsatisfying equilibrium conditions algorithm changes the height to a different position, e.g. slightly higher within the passive zone, near the toe, and lower within the active zone, near the crest of the slope.
The solution adopts the following expressions:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where: | φi | - | angle of internal friction of soil on the slip surface segment |
ci | - | soil cohesion on the slip surface segment | |
αi | - | inclination of the slip surface segment |
Equation (1) represents the relationship between the effective and total value of the normal force acting on the slip surface. Equation (2) corresponds to the Mohr-Coulomb condition representing the relation between the normal and shear forces on a given segment of the slip surface. Equation (3) represents the force equation of equilibrium in the direction normal to the ith segment of the slip surface, whereas Equation (4) represents equilibrium along the ith segment of the slip surface. SF is the factor of safety, which is used to reduce the soil parameters. Equation (5) corresponds to the moment equation of equilibrium about point M, where ygi is the vertical coordinate of the point of application of the weight of block, and yM is the vertical coordinate of point M.
Modifying equations (3) and (4) provides the following recursive formula (6):
| (6) |
This formula allows calculating all forces Ei acting between blocks for given values of δiand SF. This solution assumes that at the slip surface origin the value of E is known and equal to E1=0.
Formula for calculating angles δi (7) follows from the moment equation of equilibrium (5) as:
| (7) |
This formula allows us calculating for a given value of δ all arms zi of forces acting between blocks, knowing the value on the left at the slip surface origin, where z1 = 0.
The factor of safety FS is determined by employing the following iteration process:
- The initial value of angles is set to zero δi = 0 and positions zi to approximately one-third of interface height.
- The factor of safety FS for a given value of δi follows from equation (6) while assuming the value of En+1 = 0 at the end of the slip surface.
- The value of δi is provided by equation (7) using the values of Ei determined in the previous step.
- Steps 2 and 3 are then repeated until the value of FS does not change.
It is necessary to avoid unstable solutions for a successful iteration process. Such instabilities occur at points where division by zero in expression (6) takes place, i.e.:
![]()
Another check preventing numerical instability is verification of the parameter mα - following condition must be satisfied:
![]()
Therefore before the iteration runs, it is required to find the highest of critical values SFmin satisfying above mentioned conditions. Values below this critical value SFmin are in the area of unstable solution, therefore iteration begins by setting SF to a value "just" above SFmin and all result values of SF from iteration runs are higher than SFmin.
Generally, rigorous methods converge worse than the simpler methods (Bishop, Fellenius). Examples with convergence problems include too steep sections of slip surface, complex geometry, a significant jump in surcharge etc. If no result is obtained, we recommend a slight change of input data, e.g. less steep slip surface, input more points into the slip surface etc. or using some of the simpler methods.
Literature:
Janbu, N. 1954. Application of Composite Slip Surface for Stability Analysis. European Conference on Stability Analysis, Stockholm, Sweden.
Janbu, N. 1973. Slope Stability Computations. Embankment Dam Engineering - Casagrande Volume, R.C. Hirschfeld and S.J. Poulos, eds., John Wiley and Sons, New York, pp 47-86.