Theory of Structural Strength
The structural strength represents the resistance of soil against deformation for a load at the onset of failure of its internal structure. With decreasing coefficient m the soil responds tends to be linear.
If the structural strength is accounted for during settlement analysis, then:
a) the influence zone is characterized by the depth below the footing bottom at which the increment of vertical stress σz becomes equal to the structural strength of soil (determined by multiplying the original geostatic stress σor by the coefficient m):
![]()
where: | m | - | coefficient of structural strength |
σor | - | original geostatic stress |
b) when computing the settlement of a layer, the increment of vertical stress σz due to surcharge and reduced by the structural strength of the soil is provided by:
![]()
where: | m | - | coefficient of structural strength |
σor | - | original geostatic stress | |
σz | - | incremental stress in the middle layer |
and the settlement s then follows from the stress denoted in figure by hatching and is given by:
![]()
where: | m | - | coefficient of structural strength |
σor | - | original geostatic stress | |
σz | - | incremental stress in the middle layer |
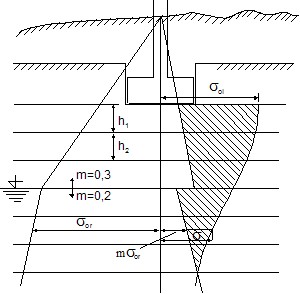 Depth of influence zone based on theory of structural strength (area of effective surcharge is hatched)
Depth of influence zone based on theory of structural strength (area of effective surcharge is hatched)