Posouzení členěných průřezů
Posouzení členěného průřezu začíná jeho zatříděním. Zatřídění se provádí stejně jako u průřezů celistvých. Posouzení členěného průřezu probíhá postupně v pořadí, jak následují oddíly tohoto textu.
Posouzení namáhání posouvající sílou Qz
Je-li osa z kolmá ke hmotné ose průřezu (a to většinou je), posuzuje se působení posouvající síly Qz v programu obdobně jako u celistvých průřezů. Smyková únosnost ve směru osy z se počítá ze vztahu
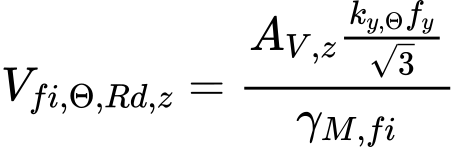
kde je: | AV,z |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Vlastní podmínka posouzení má tvar
![]()
Pokud tato podmínka není splněna, průřez nevyhovuje.
Posouzení namáhání posouvající sílou Qy
Síla Qy u většiny členěných průřezů v programu působí ve směru hmotné osy průřezu. Z toho plyne, že tato posouvající síla je z větší části přenášena tuhostí spojek. Její vliv se projevuje v posouzení únosnosti na ohyb, na vzpěr a v posouzení spojek.
Posouzení únosnosti v tahu, tlaku a ohybu
Únosnost dílčího prutu v tahu, resp. v prostém tlaku se vypočte ze vztahu
![]()
kde je: | A |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Je-li prut současně namáhán ohybovým momentem My, vypočte se ještě únosnost dílčího prutu na ohyb od momentu My. Ta je dána následujícím vztahem pro 1. a 2. třídu
![]()
Pro 3. třídu vztahem
![]()
a pro 4.třídu vztahem
![]()
kde je: | Wpl,y |
|
Wy |
| |
Wy,eff |
|
Je-li prut současně namáhán ohybovým momentem kolem nehmotné osy Mz, provede se přepočet tohoto momentu na přírůstek osové síly v dílčím prutu dN. Tento přepočet se pro průřezy s příhradovými spojkami provádí podle vztahu
![]()
pro průřezy s rámovými spojkami podle vztahu
![]()
kde je: | h0 |
|
A |
| |
Iz |
|
Je-li prut současně namáhán posouvající silou Vy ve směru hmotné osy průřezu, provede se přepočet této posouvající síly na ohybový moment Mznamáhající dílčí průřez. Pro tento přepočet je použito vztahu
![]()
kde je: | l1 |
|
Únosnost dílčího prutu na ohyb od momentu Mz se pak vypočte následujícím vztahem pro 1. a 2. třídu
![]()
Pro 3. třídu vztahem
![]()
a pro 4.třídu vztahem
![]()
kde je: | Wpl,z |
|
Wz |
| |
Wz,eff |
|
Posouzení dílčího průřezu na namáhání osovou silou a ohybovými momenty se provádí podle podmínky obdobné jako pro celistvé průřezy. Pro členěné průřezy je použita podmínka ve tvaru
![]()
kde je: | n |
|
dN |
| |
Mz,Sd |
|
Posouzení vzpěrné únosnosti
Vzpěrná únosnost při vybočení kolmo ke hmotné ose je dána vztahem
![]()
kde je: | χfi,y |
|
A |
| |
ky,θ |
| |
fy |
| |
γM,fi |
| |
βA |
|
Pro vybočení kolmo ke hmotné ose y je štíhlost λy dána vztahem
![]()
kde je: | Lcr,y |
|
iy |
|
Poměrná štíhlost ![]() je dána vztahem
je dána vztahem
![]()
kde je: | λy |
|
λ1 |
| |
βA |
| |
ky,θ |
| |
kE,θ |
|
Hodnota štíhlosti λ1 pro výpočet poměrné štíhlosti je spočtena vztahem
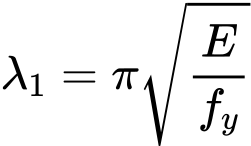
kde je: | E |
|
fy |
|
Součinitel vzpěrnosti χfi,y odpovídá poměrné štíhlosti ![]() a je pak počítán ze vztahu
a je pak počítán ze vztahu
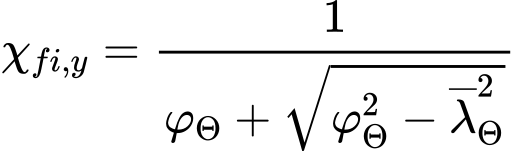
kde
![]()
kde
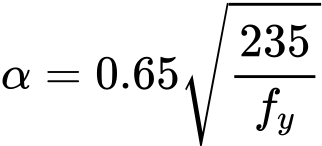
Pokud je zadaná osová síla v průřezu větší než únosnost Nfi,θ,b,Rd,y, průřez nevyhovuje.
Dále se posuzuje vzpěrná únosnost při vybočení kolmo k nehmotné ose. Je vypočtena kritická síla Ncr podle vztahu
![]()
kde je: | lcr,z |
|
kE,θ |
| |
E |
| |
Ieff |
|
Pro příhradové spojky je Ieff počítán ze vztahu
![]()
kde je: | A |
|
h0 |
|
Pro rámové spojky se nejdřív spočte moment setrvačnosti průřezu I1 podle vztahu
![]()
kde je: | A |
|
h0 |
| |
Iz |
|
Pak se spočítá poloměr setrvačnosti průřezu i0
![]()
Pro hodnotu štíhlosti danou vztahem
![]()
se přiřadí hodnota součinitele μ a moment setrvačnosti Ieff se spočte podle vztahu
![]()
Pokud je zadaná osová síla větší než kritická síla Ncr, průřez nevyhovuje.
Dalším krokem je výpočet smykové tuhosti SV. Pro rámové spojky je smyková tuhost dána vztahy
![]()
případně
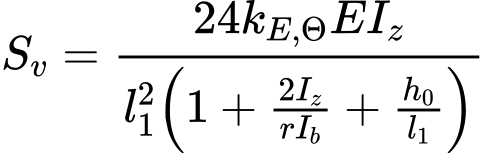
ale musí být splněno že
![]()
kde je: | l1 |
|
r |
| |
Ib |
| |
h0 |
|
Je-li zadaná osová síla větší než smyková tuhost SV, průřez nevyhovuje a výpočet končí. Je-li dále
![]()
průřez rovněž nevyhovuje.
Síla v dílčím prutu uprostřed délky mezi spojkami je pro rámové spojky dána vztahem
![]()
pro spojky příhradové pak vztahem
![]()
v nichž moment MS je určen vztahem
![]()
kde je: | e0 |
|
Vzpěrná únosnost prutu je dána vztahem
![]()
kde je: | χz |
|
βA |
| |
A |
| |
ky,θ |
| |
fy |
| |
γM,fi |
|
kde součinitel vzpěrnosti χz je určen pomocí štíhlosti λ dané vztahem
![]()
kde je: | l1 |
|
imin |
|
Poměrná štíhlost ![]() je dána vztahem
je dána vztahem
![]()
kde
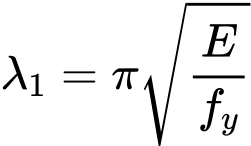
Součinitel vzpěrnosti χz odpovídá poměrné štíhlosti ![]() a je pak počítán ze vztahu
a je pak počítán ze vztahu
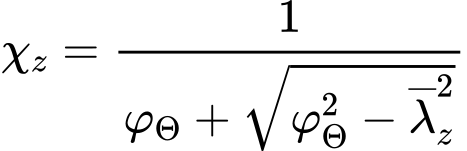
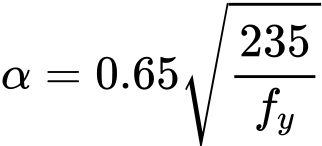
kde
![]()
kde
V místě spojky se vypočítává smyková síla VS
![]()
a moment Mz,Sd působící na dílčím průřezu vlivem spojek
![]()
kde je: | l1 |
|
Vy |
|
Únosnost dílčího prutu na ohyb od momentu My je dána následujícím vztahem pro 1. a 2. třídu
![]()
Pro 3. třídu vztahem
![]()
a pro 4.třídu vztahem
![]()
kde je: | Wpl,y |
|
Wy |
| |
Wy,eff |
|
Únosnost dílčího prutu na ohyb od momentu Mz je dána následujícím vztahem pro 1. a 2. třídu
![]()
Pro 3. třídu vztahem
![]()
a pro 4.třídu vztahem
![]()
kde je: | Wpl,z |
|
Wz |
| |
Wz,eff |
|
Posouzení se nakonec provádí ve dvou řezech. Uprostřed délky dílčího prutu a v místě spojky.
Uprostřed délky dílčího prutu se využívá podmínky
![]()
kde je: | n |
|
dN |
| |
ky |
|
V místě spojky má podmínka tvar
![]()
Posouzení příhradových spojek
Pokud se počítá bez uvažování vzpěru, získává se síla ve spojce vztahem
![]()
kde je: | Vy |
|
d |
| |
r |
| |
h0 |
|
Únosnost spojky se stanoví výrazem
![]()
kde je: | ky,θ |
|
Ad |
| |
fy |
| |
γM,fi |
|
Spojky vyhoví, platí-li
![]()
Při uvažování vzpěru se síla ve spojce získá vztahem
![]()
kde je: | Vy |
|
VS |
| |
d |
| |
r |
| |
h0 |
|
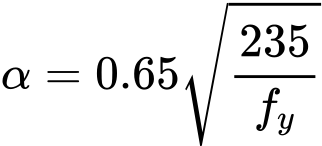
Štíhlost spojky je určena odhadem, podle vztahu
![]()
kde je: | d |
|
Ad |
|
Poměrná štíhlost ![]() je dána vztahem
je dána vztahem
![]()
kde
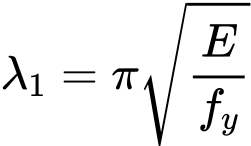
Součinitel vzpěrnosti χSp odpovídá poměrné štíhlosti ![]() a je pak počítán ze vztahu
a je pak počítán ze vztahu
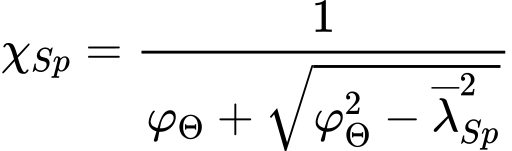
kde
![]()
kde
Vzpěrná únosnost spojky je pak dána vztahem
![]()
Spojky vyhoví, platí-li
![]()