Hardening soil
Модель Hardening soil, представленная Шанцем и др. [1] подходит для моделирования широкой группы мягких грунтов. Эта модель комбинирует два механизма упрочнения. Механизм упрочнения по сдвигу приводит к развитию пластических деформаций, вызванных девиаторными компонентами напряжения, в то время как механизм упрочнения по сжатию активируется при сжимающей нагрузке, например в одометре или при объёмном сжатии. Механизм упрочнения по сдвигу выражен постепенным развитием псдвиговой поверхности текучести в зависимости от действующего значения эквивалентной девиаторной пластической деформации κs (или γps).
Процесс упрочнения (расширения поверхности текучести) сопровождается развитием мобилизованного угла внутреннего трения φm и прерывается по достижении предела сдвиговой поверхности текучести fsMN. В программе GEO5 МКЭ эта функция текучести представлена критерием разрушения Матцуока-Накаи, являющимся функцией пиковых значений параметров прочности на сдвиг, удельного сцепления грунта c и угла внутреннего трения φ. Проекция поверхности текучести на девиаторную плоскость как соледствие это выпуклая крива, проходящая через все вершины модели MoМора-Кулона. Следствие упрочнения по сжатию это развитие шатровой поверхности текучести fcHS в зависимости от развития давления переуплотнения pc. Схожая формулировка на языке инвариантных измерений напряжения также представлена в [2].
Графическое представление обоих поверхностей текучести представлена на рисунке снизу. Постепенное развитие сдвиговой поверхности текучести становится явным, если спроецировать её на меридианную плоскость, также представленной на рисунке. Аналогичным образом опредяется и модель Soft soil, которая однако использует только предельную поверхность сдвига. Упрочнение как следствие ограничено шатрововой поверхностью сжатия.
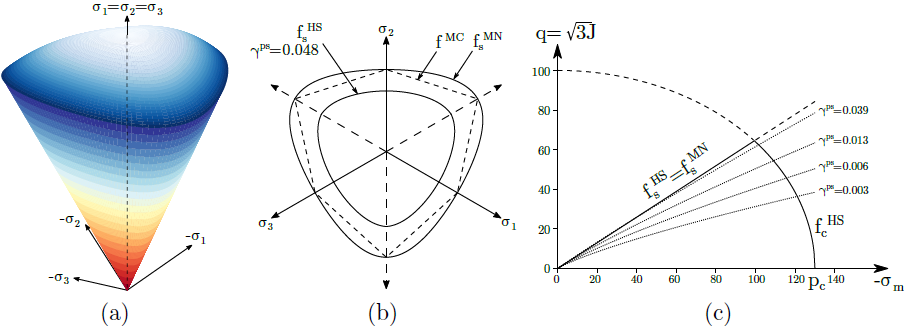 a) поверхность текучести в пространстве главных напряжений, b) проекция на девиаторную и c) меридианную плоскости
a) поверхность текучести в пространстве главных напряжений, b) проекция на девиаторную и c) меридианную плоскости
Формулировка поверхности текучести восходит к принятию того, что отношение между девиаторным напряжением q и вертикальной относительной деформацией ε3 во время трёхосных испытаний могут быть описаны при помощи гиперболической функции. Соответствующая диаграмма напряжений и относительных деформаций представлена ниже. Обращаясь к ней, мы видим следующие значения: qa - значение асимптоты для q, а qfMC сходится со значением q, когда достигает предела текучести. В этом случае выполняется равенство qf = Rfqa, где Rf - поправочный коэффициент. Более подробное объяснение вы можете найти в теоретическом руководстве.
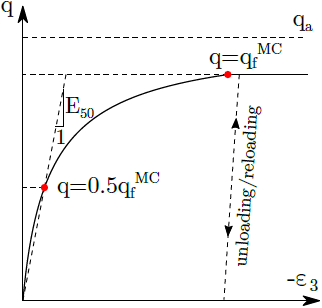 Гиперболический закон зависимости напряжений от деформации
Гиперболический закон зависимости напряжений от деформации
Параметры, определяющие модель Hardening soil, обобщены в таблице снизу.
Обозначение | Ед. изм | Описание | |
| [МПа] | Секущий модуль деформации при 50% прочности | |
| [МПа] | Модуль деформации по вторичной ветви нагружения | |
| [-] | Коэффициент Пуассона | |
| [кПа] | Относительное среднее напряжение | |
| [-] | Экспонента степенной зависимости жесткости | |
| [кПа] | Предельное значение среднего напряжения для обеспечения жесткости отличной от нуля | |
| [кН/м3] | Удельный вес грунта | |
| [-] | Начальное значение пористости соответствующее НДС на конец 1-го этапа расчёта | |
| [-] | Поправочный коэффициент несущей способности | |
| [кПа] | Эффективное удельное сцепление | |
| [°] | Эффективный угол внутреннего трения | |
| [°] | Угол дилатансии | |
| [-] | Коэффициент бокового давления нормально консолидированного грунта в покое | |
| [МПа] | Касательный одометрический модуль деформации | |
| [кПа] | Относительное вертикальное напряжение для определения | |
| [-] | Максимальное значение коэффициента пористости для прекращения дилатансии (если функция включена) | |
| [-] | Коэффициент переуплотнения | |
| [кПа] | Давление предуплотнения | |
| [1/K] | термический коэффициент расширения (в случае, если рассматривается в расчете) | |
| [-] | Параметр, определяющий форму шатровой поверхности сжатия | |
| [Па] | Модуль упрочнения (не вводится пользователем) | |
| [кПа] | Давление переуплотнения | |
| [°] | Критическое значение угла внутреннего трения (не вводится пользователем) | |
| [°] | Мобилизованный угол внутрееннего трения (не вводится пользователем) | |
| [°] | Мобилизованный угол дилатансии (не вводится пользователем) |
Секущий модуль деформации Eip,ref может быть получен при помощи модуля деформации при 50% прочности E50p,ref по формуле:
![]()
где индекс (p,ref) отражает относительное значение модуля деформации соответствующее определенному значению эффективного среднего среднего напряжения σmref. В общем случае, модель грунта учитывает развитие модуля деформации как функцию от текущего значения среднего напряжения по формуле:
![]()
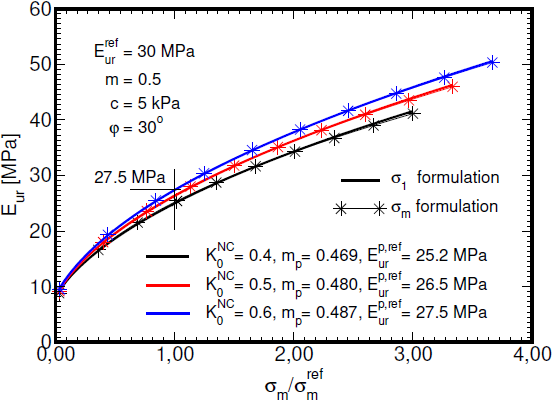
Подчеркиваем, что данная формулировка несколько отличается от тех, что изложены в источниках [1] и [2], где развитие жесткости зависит от минимального главного напряжения, в данном случае σ1. Это должно быть учтено при адаптации параметров, настроенных под другие расчетные программы, для GEO5 МКЭ. Потенциальная возможность - это использовать модифицированный набор параметров, получаемый в специальном программном обеспечении, который бы обеспечил приемлемое соответствие моделей. С этой целью парная линейная регрессия является достаточной, чтобы подогнать параметры Eurp,ref и mp. Данный подход проиллюстрирован на диаграмме снизу.
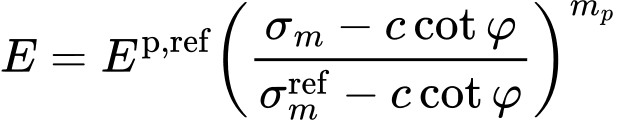 Определение зависимости модуля деформации по вторичной ветви нагружения Eur от среднего напряжения σm с использованием парной линейной регрессии
Определение зависимости модуля деформации по вторичной ветви нагружения Eur от среднего напряжения σm с использованием парной линейной регрессии
Модифицированные параметры E50p,ref(Eip,ref) и Rf могут быть получены впоследствии в рамках шага оптимизации при помощи сравнения численных симуляций испытания методом трехосного сжатия до тех пор пока не будет обеспечена сходимость с уже известными знчениями Eurp,ref и mp.
Подробная информация может быть получена в теоритическом руководстве. Однако настоятельно рекомендуется калибровать специфические параметры моделей в рамках конкретных задач на основе проведенных лабораторных измерений, использующих специальное программное обеспечение, например ExCalibre.
Шатровая поверхность сжатия fcHS характеризуется параметром M, определяющим её форму, а также модулем упрочнения H, обеспечивающим возрастание давления переуплотнения Δpc в выражении возрастания объемной пластической деформации Δεvpl. Модуль H упрочнения выражается как
где Kc, Ks - модули объемной упругости по первичной линии нагружения/разгрузки соответственно. Более подробную информацию можно найти в теоретическом руководстве. Параметры ![]() могут быть также введены напрямую или определены автоматически на основе значения коэффициента бокового давления покоя для нормально консолидированного грунта K0NC, а также касательного одометрического модуля деформации Eoedref. Это достигается при помощи численной оптимизации компрессионных испытаний. Целью оптимизации является получение параметров модели M, H таким образом, чтобы численно предсказанное значение касательного одометрического модуля деформации соответствовало значению, определенному при заданном K0NC, как это следует из рисунка снизу. Среднее напряжение σm* и эквивалентное девиаторное напряжение J* вычисляются по формулам:
могут быть также введены напрямую или определены автоматически на основе значения коэффициента бокового давления покоя для нормально консолидированного грунта K0NC, а также касательного одометрического модуля деформации Eoedref. Это достигается при помощи численной оптимизации компрессионных испытаний. Целью оптимизации является получение параметров модели M, H таким образом, чтобы численно предсказанное значение касательного одометрического модуля деформации соответствовало значению, определенному при заданном K0NC, как это следует из рисунка снизу. Среднее напряжение σm* и эквивалентное девиаторное напряжение J* вычисляются по формулам:

Более подробную информацию можно найти в теоретическом руководстве.
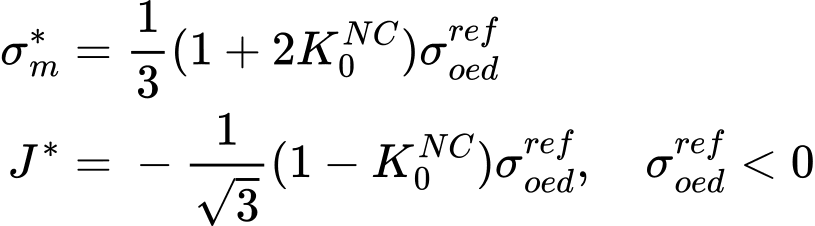 a) графическое представление отношения касательного одометрического модуля деформации Eoedref в точке при определенном σoedref, b) текущее напряжение в конце этапа оптимизации, связанная с σoedref
a) графическое представление отношения касательного одометрического модуля деформации Eoedref в точке при определенном σoedref, b) текущее напряжение в конце этапа оптимизации, связанная с σoedref
Модель Hardening soil позволяет моделировать диалатансию грунта (развитие позитивных объемных пластических деформаций) при помощи угла дилатансии ψ. Развитие пластических деформаций вызывано потенциалом пластической деформации gsHS. Определение потенциала пластической деформации фактически идентично тому, что применяется в модели Drucker-Prager. Единственное видимое различие в определении угла наклона пластического потенциала Mψ, который теперь зависит от текущего значения мобилизованного угла внутреннего трения ψm. Соответствующее динамическое уравнение строится на теории дилатансии Ровэ, что схоже с обобщенной моделью Мора-Кулона
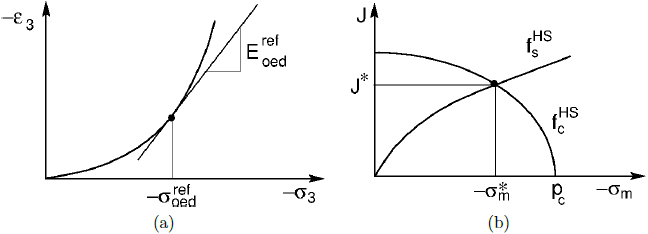
где φ, φm, φcs, ψ - значение угла внутреннего трения, мобилизованного угла внутреннего трения, критического значения угла внутреннего трения и угла дилатансии. Графическое представление ψm развития отражается в рисунке снизу. Он также иллюстрирует отсечку дилатансии, вводя максимальное значение коэффициента пористости emax, по достижении которой ожидается критическое состояние ψm = 0.
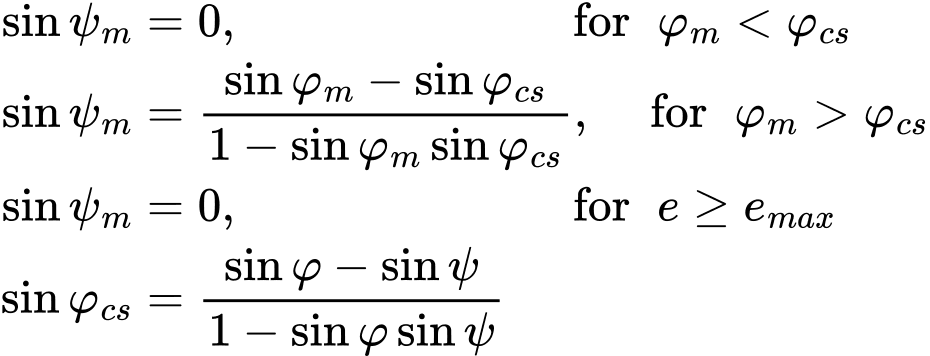 Теория дилатансии Ровэ: a) графическое представление развития мобилизованного угла дилатансии ψm, b) отсечка дилатансии
Теория дилатансии Ровэ: a) графическое представление развития мобилизованного угла дилатансии ψm, b) отсечка дилатансии
Можно обратить внимание, что развитие жесткости зависит от текущего значения эффективного среднего напряжения σm. Это тесно связано с начальным шагом решения, который должен быть достаточно малым для очень малых значений начального напряжения. Чтобы ускорить конвергенцию бывает полезным использовать минимальное число итераций для единичного шага нагрузки. Влияние амплитуды начального шага нагрузки на развитие напряжения и деформации детально изложено по ссылке.
Важный шаг для осуществления успешного расчета связана с настройкой значений начального давления переуплотнения pcin и эквивалентной пластической девиаторной деформации κsin. Оба параметра находятся в зависимости от текущего напряженного состояния таким образом, чтобы текущее напряженное состояние удовлетворяло сдвиговой и шатровой функциям текучести. Детальное объяснение приведено по ссылке. Также можно обратиться к описанию модели грунта Модифицированный Cam clay.
Модель позволяет привязать начальное значение давления переуплотнения в зависимости от ожидаемой степени переуплотнения при помощи параметров ![]() и
и ![]() . Более подробное объяснение можно получить по ссылке. Отметим, что эта опция доступна только в том случае, если начальное геостатическое давление определяется при помощи K0 процедуры.
. Более подробное объяснение можно получить по ссылке. Отметим, что эта опция доступна только в том случае, если начальное геостатическое давление определяется при помощи K0 процедуры.
Для недренированных условий расчет расчет может выполняться только в эффективных напряженияхanalysis in effective stress (cef, φe).
Модель Hardening soil также позволяет осуществить расчет устойчивости. Однако опция доступна только включен режим расчета устойчивости на стадиях НДС. В этом случае шатровая поверхность сжатия выключается как и развитие мобилизованного угла внутреннего трения. Следовательно, только сдвиговая поверхность текучести может быть активной. Задача решается путем постепенного уменьшения параметров сдвиговой прочности c, φ, как и в случае модели Drucker-Prager.
Работа модели на примере простых лабораторных испытаний продемонстрирована по ссылке, включая влияние амплитуды начального шага нагрузки.
Кроме того, есть экспериментально подтвержденные данные, что параметры модели Hardening soil должны находиться в границах, указанных в таблице снизу.
Обозначение | Ед. изм. | Рекомендуемое значение | |
| [МПа] | (2, 70) | |
| [МПа] |
| |
| [кПа] | 100.0 | |
| [-] | (0.3, 0.9) | |
| [кПа] | 10.0 | |
| [-] | 0.9 | |
| [°] | (16.0, 42.0) | |
| [кПа] | (0.0, 50.0) | |
| [°] |
| |
| [-] | (0.5, 2.5) | |
| [-] | 0,2 | |
| [-] |
| |
| [-] |
| |
| [кПа] | 100.0 | |
| [МПа] |
|
Реализация модели Hardening soil в программе GEO5 МКЭ детально описана в теоретическом руководстве.
Источники:
[1] T. Schanz, P.A. Vermeer, P.G. Bonnier, The hardening soil model: Formulation and verification, Beyond 2000 in Computational Geotechnics, Balkema, Rotterdam. 1999
[2] T. Benz, Small-Strain Stiffness of Soils and its Numerical Consequences, PhD thesis, University of Stuttgart, 2007