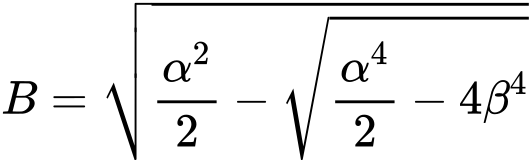Geometric Method (Euler)
The soil surrounding the micropile is represented in the program by the modulus of subsoil reaction Ep (Winkler constant k) defined by the user in the frame "Verification of cross-section". A model of a structure is displayed in the figure.
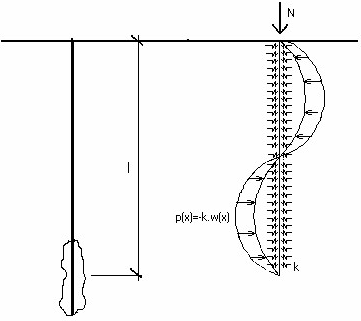Model of structure
For a micropile in compression it is expected that a varying number of half-waves occurs depending on the geometry and stiffness of the structure and surrounding soil, respectively. The solution to this case arises from the equation of bending of a straight beam.
After some manipulations the bending equation can be expressed as:
| |
where: | |
| |
| |
| |
|
Integration constants C1-C4 are found from four boundary conditions depending on the assumed endpoint supports.
The critical force Ncr is calculated from the formula (in [1]):
where: | Ei | - | modulus of elasticity of a ideal cross-section |
Ii | - | moment of inertia of a ideal cross-section | |
lp | - | effective micropile length (free length + 1/2 root length) | |
Er | - | ||
n | - | number of half-waves |
The critical force Ncr is taken as a minimum of function (1). It is achieved for the length of half-wave:
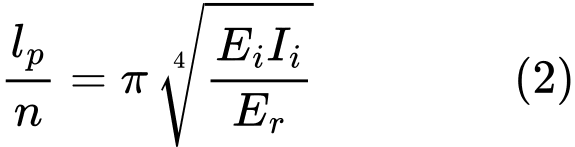
The number of half-waves n is based on formula (2):
If the part of micropile is above the terrain (pile head offset), the reduced values n a Er are calculated as follows:
where: | lv | - | length of micropile above the terrain |
Assuming hinge-hinge condition,the following equation is used:
Assuming hinge-fixed condition, the following equation is used:
Literature:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936