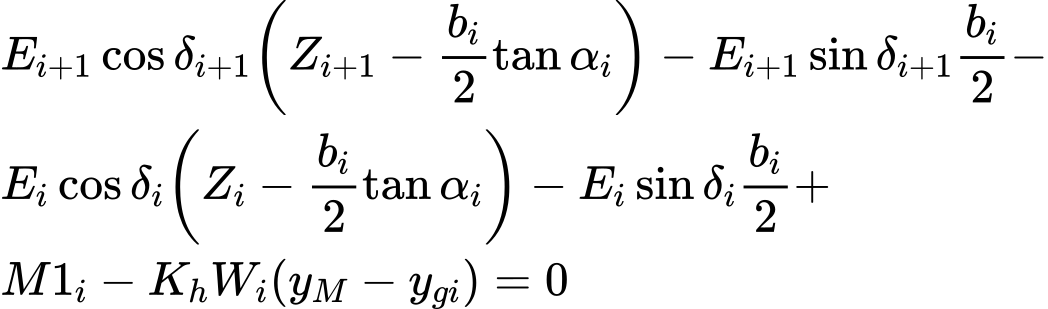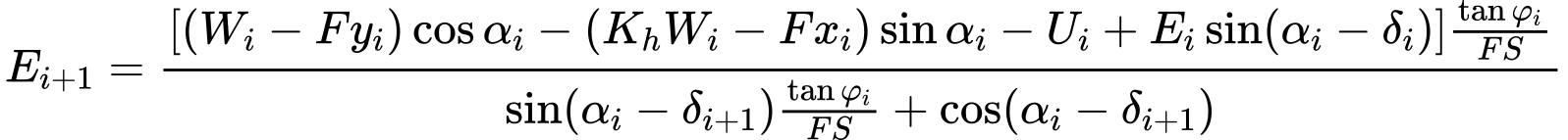Morgenstern-Price
Morgenstern-Price is a general method of slices developed on the basis of limit equilibrium. It requires a satisfying equilibrium of forces and moments acting on individual blocks. The blocks are created by dividing the soil above the slip surface by dividing planes. Forces acting on individual blocks are displayed in the following figure:
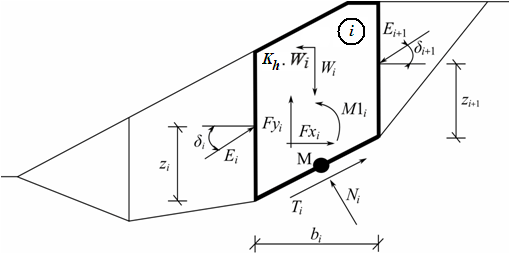Static scheme - Morgenstern-Price method
Each block is assumed to contribute due to the same forces as in Spencer method. The following assumptions are introduced in the Morgenstern-Price method to calculate the limit equilibrium of forces and moment on individual blocks:
- dividing planes between blocks are always vertical
- the line of action of the weight of block Wi passes through the center of the ith segment of slip surface represented by point M
- the normal force Ni is acting in the center of the ith segment of slip surface, at point M
- inclination of forces Ei acting between blocks is different on each block (δi) at slip surface endpoints is δ = 0
The only difference between Spencer and Morgenstern-Price method is shown in the above list of assumptions. Choice of inclination angles δi of forces Ei acting between the blocks is realized with the help of Half-sine function - one of the functions in the following figure is automatically chosen. This choice of the shape of function has a minor influence on final results, but a suitable choice can improve the convergency of the method. The functional value of Half-sine function f(xi) at boundary point xi multiplied by parameter λ results in the value of inclination angle δi.
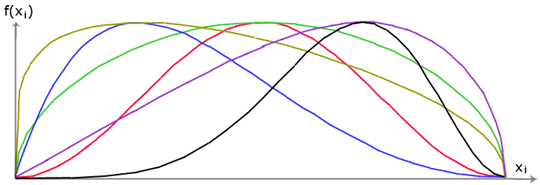Half-sine function
The solution adopts the expressions (1) - (5), shown in Spencer method, i.e.:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where: | φi | - | angle of internal friction of soil on the slip surface segment |
ci | - | soil cohesion on the slip surface segment | |
αi | - | inclination of the slip surface segment |
- (1) relationship between the effective and total value of the normal force acting on the slip surface
- (2) Mohr-Coulomb condition representing the relation between the normal and shear forces on a given segment of the slip surface (Ni a Ti)
- (3) force equation of equilibrium in the direction normal to the ith segment of the slip surface
- (4) force equation of equilibrium along the ith segment of the slip surface
- (5) moment equation of equilibrium about point M
Modifying force equations (3) and (4) provides the following recursive formula (6):
| (6) |
This formula allows calculating all forces Ei acting between blocks for given values of δi and SF. This solution assumes that at the slip surface origin the value of E is known and equal to E1 = 0.
Additional recursive formula (7) follows from the moment equation of equilibrium (5) as:
| (7) |
This formula allows us to calculate all arms zi of forces acting between blocks for a given value of δi, knowing the value on the left at the slip surface origin, where z1 = 0.
The factor of safety SF is determined by employing the following iteration process:
- The initial value of angles δi is set according to the half-sine function (δi = λ*f(xi)).
- The factor of safety SF for a given value of δi follows from equation (6) while assuming the value of En+1 = 0 at the end of the slip surface.
- The value of δi is provided by equation (7) using the values of Ei determined in the previous step with the requirement of having the moment on the last block equal to zero. Functional values f(xi) are the same all the time during the iteration, only parameter λ is iterated. Equation (7) does not provide the value of zn+1 as it is equal to zero. For this value, the moment equation of equilibrium (5) must be satisfied.
- Steps 2 and 3 are then repeated until the value of δi (resp. parameter λ) does not change.
It is necessary to avoid unstable solutions for successful iteration process. Such instabilities occur at points where division by zero in expressions (6) and (7) takes place. In equation (7), division by zero is encountered for δi= π/2 or δi = -π/2. Therefore, the value of angle δimust be found in the interval (-π/2 ; π/2).
Division by zero in expression (6) appears when:
Another check preventing numerical instability is verification of the parameter mα - following condition must be satisfied:
Therefore before theiteration runs, it is required to find the highest of critical values SFmin satisfying above-mentioned conditions. Values below this critical value SFmin are in an area of unstable solution, therefore iteration begins by setting SF to a value "just" above SFmin and all result values of SF from iteration runs are higher than SFmin.
Generally, rigorous methods converge worse than the simpler methods (Bishop, Fellenius). Examples with convergence problems include too steep sections of slip surface, complex geometry, a significant jump in surcharge etc. If no result is obtained, we recommend a slight change of input data, e.g. less steep slip surface, input more points into the slip surface etc. or using some of the simpler methods.
Literature:
Morgenstern, N.R., and Price, V.E. 1965. The analysis of the stability of general slip surfaces. Géotechnique, 15(1): 79-93.
Morgenstern, N.R., and Price, V.E. 1967. A numerical method for solving the equations of stability of general slip surfaces. Computer Journal, 9: 388-393.
Zhu, D.Y., Lee, C.F., Qian, Q.H., and Chen, G.R. 2005. A concise algorithm for computing the factor of safety using the Morgenstern-Price method. Canadian Geotechnical Journal, 42(1): 272-278.