Online Help

Sarma

The Sarma method falls within a category of general sliced methods of limit states. It is based on fulfilling the force and moment equilibrium conditions on individual blocks. The blocks are created by dividing the soil region above the potential slip surface by planes, which may have in general experience a different inclination. Forces acting on individual blocks are displayed in the following figure.

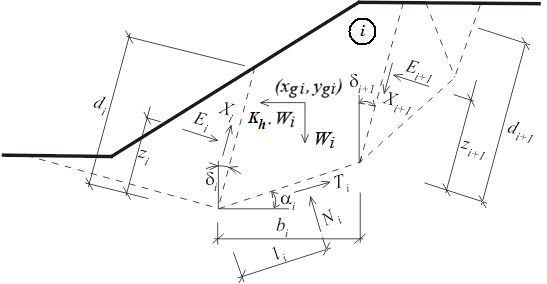Static scheme - Sarma method

Here, E_i ,X_i represent the normal and shear forces between the blocks. N_i ,T_i  are normal and shear forces on segments of a slip surface. W_i is the block weight and K_h*W_i  is the horizontal force that is used to achieve in the Sarma method the limit state. Generally, inclined surcharge can be introduced in each block. This surcharge is included in the analysis together with the surcharge due to water having the free water table above the terrain, and with forces in anchors. All these forces are projected along the horizontal and vertical directions, which are then summed up into components Fx_i and Fy_i.

K_h is a constant named the factor of horizontal acceleration and it is introduced into the analysis in order to satisfy the equilibrium on individual blocks. There is a relationship between K_h and the factor of slope stability SF allowing for the safety factor computation. In ordinary cases, the analysis proceeds with the value of K_h equal to zero. A non-zero value of K_h is used to simulate the horizontal surcharge, e.g. due to earthquake (see below).

Analysis process

Computation of limit equilibrium

The computation of limit equilibrium requires the solution of 6n - 1 unknowns, where n stands for the number of blocks dividing the soil region above the potential slip surface. These are:

5n - 1 equations are available for the required unknowns. In particular, we have:

a)horizontal force equations of equilibrium on blocks:

b)vertical force equations of equilibrium on blocks:

c) moment equations of equilibrium on blocks:

where rx_i and ry_i are arms of forces Fx_i and Fy_i

d) relationship between the normal and shear forces according to the Mohr-Coulomb theory:

It is evident that n - 1 must be selected (estimated) a priori. A relatively small error is received when estimating the points of application of forces E_i. The problem then becomes statically determined. Solving the resulting system of equations finally provides the values of all remaining unknowns. The principal result of this analysis is the determination of the factor of horizontal acceleration K_h.

Computation of factor of slope stability SF

The factor of slope stability SF is introduced in the analysis such as to reduce the soil strength parameters c and tgφ. Equilibrium analysis is then performed for the reduced parameters to arrive at the factor of horizontal acceleration K_h pertinent to a given factor of slope stability SF. This iteration is repeated until the factor K_h reaches either zero or a specified value.

Influence of external load

The analyzed slope can be loaded on its ground by inclined load having a generally trapezoidal shape. This load enters the analysis such that its vertical material component (if having the direction of weight) is added to the weight of a corresponding block. This results in change of both the slice weight and its center of gravity. Providing the vertical component acts against the direction of gravity it is added to force Fy_i. The horizontal component is added to force Fx_i.

Literature:

Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423-433, 1973.