Model Druckera-Pragera
Model materiałowy Druckera-Pragera jest najprostszym modelem materiałowym, który można zastosować do modelowania nieliniowej odpowiedzi gruntów. W przeciwieństwie do modelu Mohra-Coulomba powierzchnia plastyczności Druckera-Pragera jest gładka i w przestrzeni naprężeń głównych przedstawia kształt stożka cylindrycznego. Jak widać na poniższym rysunku, powierzchnia plastyczności, podobnie jak w modelu Mohra-Coulomba, zależy od średniego naprężenia efektywnego σmeff. Obecna wersja modelu zaimplementowana w programie GEO5 MES bazuje na założeniu trójosiowego wydłużenia. Innymi słowy, rzut powierzchni plastyczności fDP na płaszczyznę dewiatorową przechodzi przez wewnętrzne wierzchołki sześciokąta Mohra-Coulomba θ = - 30°, gdzie θ jest kątem Lode'a.
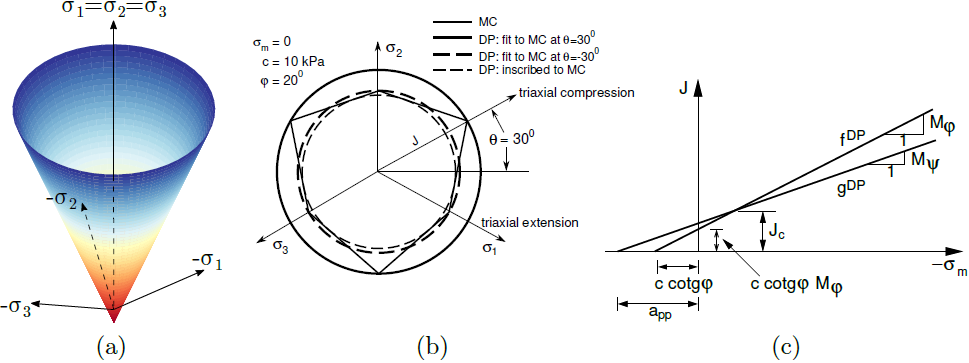 a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatorowe i c) płaszczyzny południkowe
a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatorowe i c) płaszczyzny południkowe
Model Druckera-Pragera pozwala uwzględnić dylatancję materiału (rozwój dodatnich objętościowych odkształceń plastycznych podczas ścinania plastycznego) poprzez wprowadzenie kąta dylatancji ψ. Rozwój odkształceń plastycznych jest na ogół kontrolowany przez potencjał plastyczny gDP. Podczas gdy nachylenie powierzchni plastyczności w płaszczyźnie południka jest dane przez kąt tarcia wewnętrznego Mφ = Mφ(φ), nachylenie powierzchni potencjału plastycznego zależy od kąta dylatancji Mψ = Mψ(ψ). Warunek ψ = φ odpowiada stowarzyszonemu prawu płynięcia, w przeciwnym razie rozpatrywane jest niestowarzyszone prawo płynięcia. Więcej szczegółów można znaleźć w podręczniku teoretycznym. Ponieważ grunt ostatecznie osiąga tzw. stan krytyczny (zerowy przyrost objętościowego odkształcenia plastycznego podczas ścinania plastycznego), pożądane jest ograniczenie zakresu dylatancji. Wymaga to wprowadzenia maksymalnego wskaźnika porowatości emax, dla którego oczekuje się osiągnięcia stanu krytycznego ψ = 0. Przykład ilustrujący przedstawiono tutaj. Natomiast w niniejszym artykule przedstawiono, jak dobór wartości kąta dylatancji wpływa na przewidywanie reakcji gruntu w porównaniu z jego rzeczywistym zachowaniem. Dla przejrzystości, na poniższym rysunku przedstawiono graficzną reprezentację ewolucji odkształcenia objętościowego z odcięciem dylatancji.
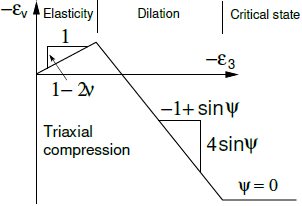 Ewolucja odkształcenia objętościowego z odcięciem dylatancji
Ewolucja odkształcenia objętościowego z odcięciem dylatancji
Podstawowe parametry materiałowe definiujące model Druckera-Pragera przedstawiono w poniższej tabeli. Parametry te można przyjąć podczas analizy w warunkach z odpływem lub w warunkach bez odpływu, Typ (1): analiza w naprężeniach efektywnych (cef, φef). W przypadku wyboru analizy Typu (2): analiza w naprężeniach efektywnych (Su) wartość spójności efektywnej c jest zastępowana wartością wytrzymałości na ścinanie w warunkach bez odpływu Su. Wartość efektywnego kąta tarcia wewnętrznego φ = φu przyjmowana jest równa zero, φ = 0. Powierzchnię plastyczności Druckera-Pragera zastępuje się następnie powierzchnią plastyczności Misesa, patrz poniżej. Zakłada się jednak, że parametry sztywności są efektywne. W warunkach bez odwodnienia na ogół oczekuje się, że grunt nie ulegnie dylatancji. Dlatego dla obydwu opcji przyjmuje się kąt dylatancji ψ = 0.
Z tabeli parametrów materiałowych wynika, że model Druckera-Pragera, podobnie jak zmodyfikowany model Mohra-Coulomba uwzględnia inną reakcję gruntu przy obciążeniu pierwotnym i przy odciążeniu/dociążeniu, poprzez wprowadzenie modułu odciążenie/dociążenie Eur, Przeczytaj także o modelu Mohra-Coulomba.
Symbol | Jednostka | Opis | |
| [MPa] | Moduł sprężystości | |
| [MPa] | Moduł odciążenie/dociążenie | |
| [-] | Współczynnik Poissona | |
| [kPa] | Efektywna spójność | |
| [°] | Efektywny kąt tarcia wewnętrznego | |
| [°] | Kąt dylatancji | |
| [kN/m3] | Ciężar objętościowy | |
| [-] | Początkowy wskaźnik porowatości odpowiadający stanowi na koniec 1. fazy obliczeń | |
| [-] | Maksymalny wskaźnik porowatości do zakończenia dylatancji (przy ograniczeniu dylatancji) | |
| [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) |
W przypadku wyboru warunków bez odpływu Typ (3): analiza w naprężeniach całkowitych Su powierzchnia plastyczności Druckera-Pragera jest także zstępowana powierzchnią plastyczności Misesa. Analogicznie, powierzchnia plastyczności Mohra-Coulomba zastępowana jest powierzchnią plastyczności Tresci. Na rysunku przedstawiono graficzną reprezentację zagadnienia. Opcja ta uwzględnia zatem φ = ψ = 0, co odpowiada stowarzyszonemu prawu płynięcia. Ponieważ modelujemy materiał objętościowo nieściśliwy, wartość współczynnika Poissona jest zwykle wybierana w zakresie (0.49 - 0.499). Należy zauważyć, że przyjęcie wartości współczynnika Poissona zbyt bliskiej 0,5 może skutkować niestabilnością numeryczną. W najlepszym przypadku wyniki będą dosyć niedokładne. Więcej informacji można przeczytać w podręczniku teoretycznym.
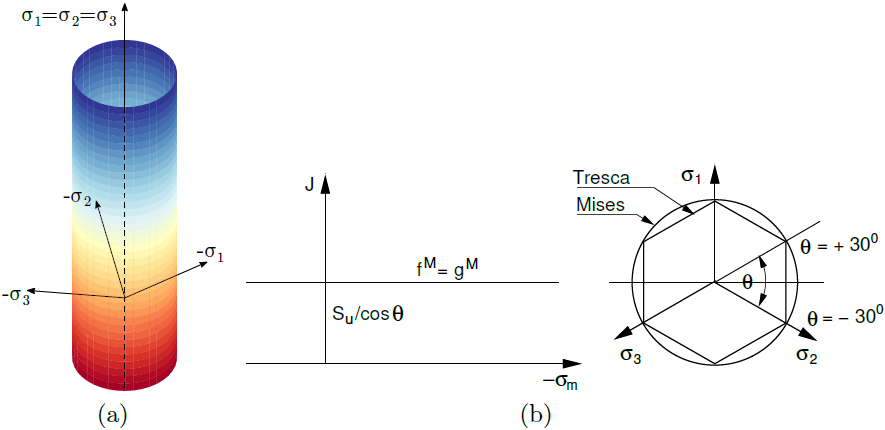 a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatoryczne i c) płaszczyzny południkowe
a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatoryczne i c) płaszczyzny południkowe
Parametry materiałowe definiujące powierzchnie plastyczności Misesa i Tresci podane są w tabeli poniżej. W przypadku powierzchni plastyczności Misesa wartość kąta Lode'a θ jest stała i równa θ = ± 30°.
Symbol | Jednostka | Opis | |
Eu | [Pa] | Moduł sprężystości w warunkach bez odpływu | |
Su | [Pa] | Wytrzymałość na ścinanie w warunkach bez odpływu | |
ν | [-] | Współczynnik Poissona przyjmowany w zakresie (0.49 - 0.499) | |
γ | [kN/m3] | Ciężar objętościowy | |
α | [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) |
Model Druckera-Pragera, podobnie jak model Mohra-Coulomba, pozwala na wykonywanie analiz stateczności. Można wykonać zarówno standardową analizę stateczności zbocza jak i analizę stateczności w obrębie danej fazy budowy. W obydwu przypadkach zadanie to rozwiązuje się poprzez stopniową redukcję parametrów wytrzymałości na ścinanie c, φ poprzez wprowadzenie parametru redukcji ζ takiego, że:
![]()
gdzie c, φ są właściwymi, rzeczywistymi parametrami wytrzymałościowymi, a cd, φd parametrami zredukowanymi. Współczynnik stateczności FS wyznaczany jest następująco
![]()
W podobny sposób redukowany jest kąt dylatancji ψ, pod warunkiem, że ψ ≠ 0.
Implementację modelu materiałowego Druckera-Pragera do programu GEO5 MES opisano szczegółowo w podręczniku teoretycznym.