Drucker-Prager
Vstupními parametry pro tento model jsou modul pružnosti zeminy E a Poissonovo číslo, dále pak úhel vnitřního tření a soudržnost zeminy, které určují hranici plasticity. Program modeluje ustálený stav po redistribuci pórových tlaků a používá tedy efektivní parametry úhlu vnitřního tření φef, a soudržnosti cef Zadává se také úhel dilatance.
Drucker-Pragerův model (někdy též rozšířený von Misesův) upravuje singularity Mohr-Coulombova modelu. Na rozdíl od Mohr-Coulombova modelu je Drucker-Pragerova plocha plasticity hladká a v prostoru hlavních napětí je zobrazena jako cylindrický kužel. Jak je patrné z obrázku, je podmínka plasticity podobně jako v případě Mohr-Coulombova modelu závislá na středním efektivním napětí σm. Verze modelu implementována v GEO MKP vychází z předpokladu triaxiálové extenze. Jinými slovy, průmět plochy plasticity do deviátorové roviny prochází vnitřními vrcholy Mohr-Coulombova hexagonu (θ = -300), kde θ je Lodeův úhel.
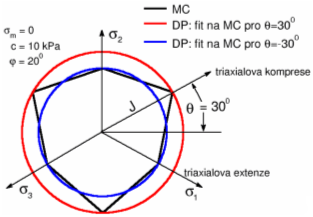 DP a MC podmínky plasticity v deviátorové rovině
DP a MC podmínky plasticity v deviátorové rovině