Modelos Materiais para a Análise de Fluxo
A análise de fluxo para estado constante é realizada segundo a lei de Darcy, que específica a relação entre a velocidade do fluxo e o gradiente hidráulico. A versão atual do programa assume valores constantes para o coeficiente de permeabilidade, independentemente da pressão nos poros.
O programa também implica que o índice de vazios iniciale0 seja definido, para a determinação da porosidade atual n e, consequentemente, da velocidade atual do fluxo de água entre os poros vs = v/n, onde v é a velocidade média do fluxo ao longo de toda a área em que se verifica percolação. Normalmente, o índice de vazios e0 = 1 corresponde a uma porosidade do solo de n = 50%.
Ao introduzir o coeficiente de permeabilidade relativa Kr o programa permite localizar a zona de transição entre uma região do subsolo totalmente saturada (S = 1, Kr = 1) e uma não saturada (Kr => 0). Como exemplo, é possível considerar o problema de fluxo não confinado. O processo de localização da zona de transição é realizado através de um dos três modelos de zonas de transição que determinam a evolução do coeficiente de permeabilidade relativa Kr em função da carga da pressão nos poros (ver Figuras).
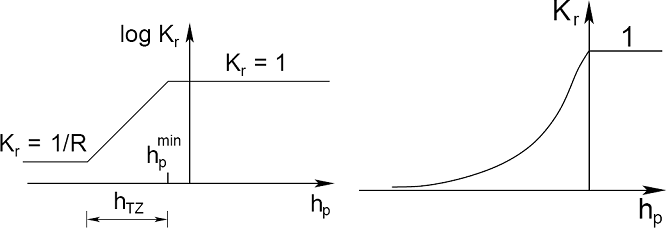 (a) Modelo log-linear [1], (b) Modelo de Van Genuchten [2]
(a) Modelo log-linear [1], (b) Modelo de Van Genuchten [2]
Modelo log-linear
O modelo da zona de transição log-linear, descrito em [1], é definido através dos parâmetros seguintes:
hpmin | - | valor mínimo da carga da pressão em região totalmente saturada [kPa] | |
hTZ | - | largura da zona de transição [m] | |
R | - | parâmetro de redução, número suficiente elevado R = 100 a 1000 [-], valor de origem assumido é R = 1000 [-] |
O coeficiente de permeabilidade relativa Kr é dado por:
![]()
Modelo de Gardner
Este é um modelo equivalente que depende apenas do parâmetro α [1/m]. O coeficiente de permeabilidade relativa Kr é, neste caso, dado por [4]:
![]()
Modelo de Van Genuchten
Neste caso, o valor do coeficiente de permeabilidade relativa Kr é dado por:
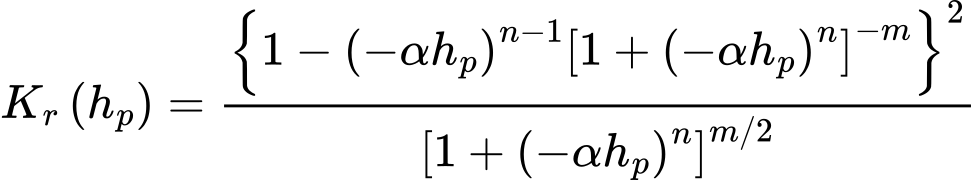
onde α [1/m], n > 1, m = 1 - 1/n são parâmetros do modelo. Os seus valores podem ser obtidos a partir de medições de laboratoriais de curvas de retenção aproximadas, através de:
![]()
![]()
onde: | Ssat | - | grau de saturação do solo totalmente saturado, valor de origem Ssat = 1 |
Sr | - | grau de saturação residual | |
Θ | - | teor de água normalizado |
O parâmetro Θ é obtido através de:
![]()
onde: | θr | - | teor de água residual [m3/m3] |
θS | - | teor de água do solo totalmente saturado [m3/m3] |
O grau de saturação atual S pode ser expresso como um rácio entre o teor de água θ e a porosidade n, da forma seguinte (é necessário distinguir o parâmetro n que representa a porosidade e o parâmetro n que aparece no modelo de van Genuchten):
![]()
Os modelos log-linear e de Gardner adotam uma versão simplificada do modelo de van Genuchten, de acordo com [5]:
![]()
onde b > 0 [-] é um parâmetro de adaptação para obter uma melhor aproximação dos dados de retenção de um solo.
As tabelas de parâmetros seguintes são utilizadas no programa. Estes parâmetros foram obtidos através das tabelas originais.
Os valores ótimos dos parâmetros do modelo de van Genuchten, para várias classificações, com base em USDA e FAO, são apresentados nas tabelas seguintes.
Tabela com coeficientes de regressão em função do tamanho das partículas USDA segundo Van Genuchten (1991)
Solo (tamanho das partículas) | Ksat [m/day] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/m] | n [-] | e [-] | Sr [-] | α [1/m] | n [-] | ||
Areia | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
Areia barrosa | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
Barro arenoso | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Barro | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Silte | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Barro siltoso | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Barro de argila arenosa | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Barro argiloso | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Barro de argila siltosa | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Argila arenosa | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Argila siltosa | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Argila | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | 0,85 | 0,21 | 1,5 | 1,253 |
Tabela com coeficientes de regressão em função do tamanho das partículas FAO segundo Van Genuchten (1998)
Solo (tamanho das partículas) | Ksat [m/day] | e [-] | Sr [-] | α [1/m] | n [-] |
Solo superior (até 1 m de profundidade) | |||||
Grosseiro (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Médio (M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Mediamente Fino (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Fino (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Muito Fino (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Solo profundo (> 1 m) | |||||
Grosseiro (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Médio (M) | 0,108 | 0,65 | 0,026 | 2,49 | 1,1689 |
Mediamente Fino (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Fino (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Muito Fino (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Tabela: sistema de classificação de textura FAO
Solo | Definição |
Grosseiro (C) Médio (M) | argila < 18% e areia > 65% 18%< argila < 35% e 15%< areia ou: argila < 18% e 15%< areia < 65% |
Mediamente Fino (MF) | argila < 35% a areia < 15% |
Fino (F) | 35%< argila < 60% |
Muito Fino (VF) | 60%< argila |
Bibliografia:
Details can be found in [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering - theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2015)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228-232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Metoda konečných prvků v geomechanice: Teoretické základy a inženýrské aplikace, předpokládaný rok vydání (2015)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.