Modificação da Matrix de Rigidez
O método de Newton-Raphson assume que a matriz de rigidez tangente instantânea é formada no início de cada nova iteração.
A formação de uma nova matriz de rigidez tangente apenas no início de um aumento de carregamento conduz à adoção do método de Newton-Raphson modificado.
Se a matriz de rigidez for formada apenas no início da análise, obtém-se o método de tensão inicial.
Cada método pode ser selecionada na caixa de diálogo "Configurações da análise", na secção "Atualização da rigidez". As opções possíveis são:
- Manter elasticidade - método de tensão inicial,
- Após cada iteração - método de Newton-Raphson,
- Após cada carregamento - método de Newton-Raphson modificado.
A configuração de origem assume o algoritmo de Newton-Raphson (rigidez atualizada após cada iteração). De notar que a formulação da matriz de rigidez está relacionada com a atualização do algoritmo da tensão. Esta formulação assegura a convergência quadrática do método de Newton-Raphson (NRM), contrariamente ao NRM modificado ou ao método de tensão inicial que, em comparação com o NRM, implica um número consideravelmente mais elevado de iterações para atingir o equilíbrio.
Por outro lado, é de referir que o custo computacional por iteração é maioritariamente determinado pelo cálculo e fatorização da matriz de rigidez tangente. Ao assumir uma resposta elástica da estrutura, não existe necessidade de definir a matriz de rigidez mais do que uma vez (atualização da rigidez - manter elasticidade). O aumento do grau de não linearidade leva a reformulações mais frequentes da rigidez (atualização da rigidez - após cada iteração).
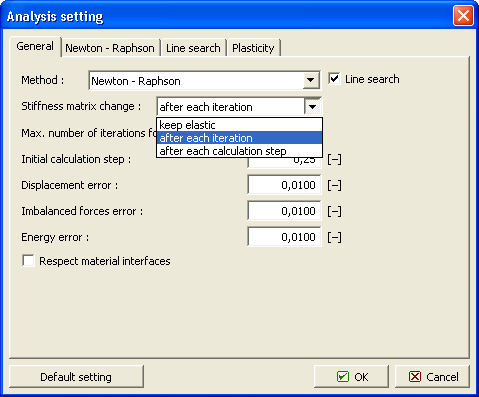 Método de Newton-Raphson - opções de atualização da matriz de rigidez
Método de Newton-Raphson - opções de atualização da matriz de rigidez