Suavização e Endurecimento
A formulação normal dos modelos de Drucker-Prager e de Mohr-Coulomb Modificado assume um comportamento elasto-plástico rígido do solo, em que os parâmetros de resistência do solo c e φ se mantêm constantes durante a análise. A seleção de ambos os modelos (nas "Opções avançadas do programa") permite a evolução destes parâmetros em função da deformação plástica de desvio equivalente:
![]()
![]()
onde: |
| - | deformação plástica de desvio equivalente, dada pelas expressões: |
![]()
![]()
![]()
onde: |
| - | deformação plástica de desvio equivalente |
| - | tensor de deformação plástica de desvio | |
| - | tensor de deformação plástica | |
| - | deformação plástica volumétrica | |
| - | delta de Kronecker |
A variação, por partes, dos parâmetros de resistência assumida é visível na Figura.
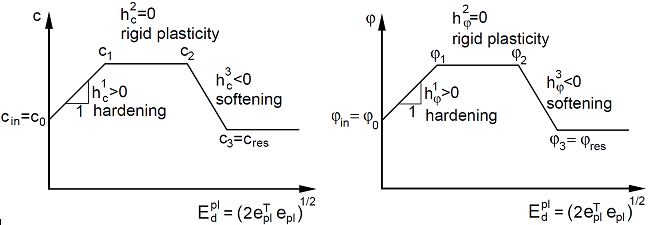 Lei multi-linear de endurecimento-suavização: em função da a) coesão e b) ângulo de atrito interno na deformação plástica de desvio equivalente Edpl
Lei multi-linear de endurecimento-suavização: em função da a) coesão e b) ângulo de atrito interno na deformação plástica de desvio equivalente Edpl
O ângulo de dilatação ψ pode ser assumido como constante ou podem desenvolver-se em função do ângulo de atrito interno φ de acordo com a teoria de dilatação de Rowes:
![]()
onde φcv é o ângulo de atrito interno para um volume constante que consiste no estado crítico do solo (estado para o qual o solo se deforma com deformações volumétricas plásticas nulas). De modo a evitar um aumento infinito do ângulo de dilatação (aumento de deformações plásticas volumétricas de tração), este deve ser relacionado, por exemplo, em função do volume de vazios máximo emax aceitável para o material. A teoria de dilatação de Rowes implica a definição dos parâmetros seguintes:
φcv | - | ângulo de atrito interno para volume constante [-] |
e0 | - | índice de vazios inicial |
emax | - | índice de vazios máximo [-] |
O índice de vazios e pode ser expresso em função da deformação volumétrica εv e do valor do volume de vazios inicial e0:
![]()
![]()
onde: | e | - | índice de vazios |
e0 | - | índice de vazios inicial | |
εv | - | deformação volumétrica global |
Quando o índice de vazios e excede o índice de vazios máximo emax, o ângulo de dilatação ψ é definido como 0.