Online Help

Shahunyants

O método de Shahunyants baseia-se na análise do estado de equilíbrio limite. Este método implica que o equilíbrio de forças e momentos seja verificada para cada bloco (excluindo o bloco superior, onde o equilíbrio de momentos não é verificado). Os blocos consistem na divisão do perfil do talude através de planos divisores. As forças atuam em cada bloco de acordo com a seguinte figura:

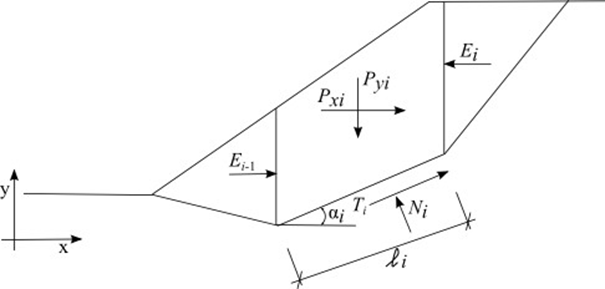Esquema das forças atuantes - Método de Shahunyants

Cada bloco estará sujeito às forças seguintes:

Para calcular o equilíbrio de forças e momentos limite através do método de Shahunyants, são consideradas as seguintes premissas:

• os planos que divisores dos blocos são sempre verticais
• a inclinação das forças E_i atuantes entre blocos é zero, as forças atuam horizontalmente

Método de resolução:

A componente das forças P_yi e P_xi é calculada através das Equações (1) e (2) de forma a obter os valores para as direções das forças T_i e N_i. Para um valor positivo do ângulo α_i (como representado no esquema) a força P_Ni atua na direção oposta a N_i e a força P_Qi atua na direção oposta a T_i.

(1)

(2)

As forças que atuam na direção da superfície de deslizamento relacionam-se de acordo com a seguinte equação:

(3)

Equações de equilíbrio para cada bloco:

Equação de equilíbrio na direção normal ao segmento da superfície de deslizamento:

(4)

Equação de equilíbrio na direção paralela ao segmento da superfície de deslizamento:

(5)

A partir das Equações (3) e (5) obtém a Equação (6):

(6)

A partir das Equações (4) e (6) obtém a Equação (7):

(7)

Desenvolvendo, obtém-se a Equação (8):

(8)

Considerando a seguinte equação trigonométrica:

(9)

E aplicando-a à Equação (8), obtém-se a Equação (10):

(10)

Que é equivalente a:

(11)

E pode ser desenvolvida de maneira a obter as foças E_i atuantes entre blocos:

(12)

Nesta fase, o fator de segurança K_u é introduzido na análise. O fator de segurança consiste no valor que torna o estado das forças que atuam em cada bloco em estados limite. Isto é conseguido através da multiplicação das forças ativas, isto é, as forças que contribuem para o deslizamento do solo acima da superfície de deslizamento, pelo fator de segurança. As forças ativas são consideradas na Equação (12), no termo P_Qi. Este termo contém tanto as forças ativas com contribuem para o deslizamento do talude como as forças estabilizadoras. As forças desestabilizadoras serão denominadas de P_Qi,sd, enquanto que as forças estabilizadoras serão denominadas de P_Qi,ud:

(13)

Se o valor de P_Qi for positivo, este contribui para o deslizamento do talude e será considerado como uma força ativa P_Qi,sd. Se o valor de P_Qi for negativo, este contribui para o aumento da resistência ao deslizamento e será considerado como uma força P_Qi,ud. Então, subtraindo o valor de P_Qi,ud, que é negativo, na Equação (13) significa somar um valor positivo, e a expressão pode ser escrita da seguinte forma:

(14)

Na origem da superfície de deslizamento o valor de E₀ = 0. Assim, o valor de E₁ é dado por:

(15)

O valor de E₂ é dado por:

(16)

As restantes forças atuantes entre blocos poderão ser determinadas de forma semelhante. Mantendo a condição de que no ponto final da superfície de deslizamento o valor de E_n = 0. Desenvolvendo a expressão anterior, obtém-se:

(17)

Esta expressão pode ser utilizada para a obtenção direta do fator de segurança K_u:

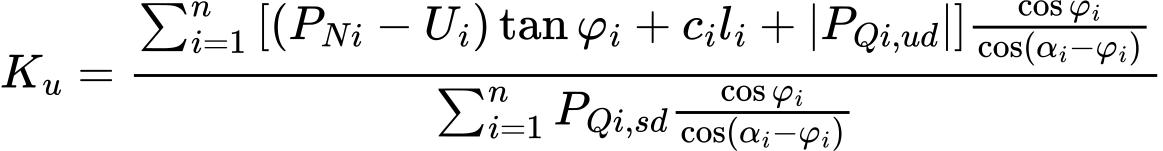(18)